
AI シグモイド関数
シグモイド関数 は ロジスティック関数 とも呼ばれます。

シグモイド関数
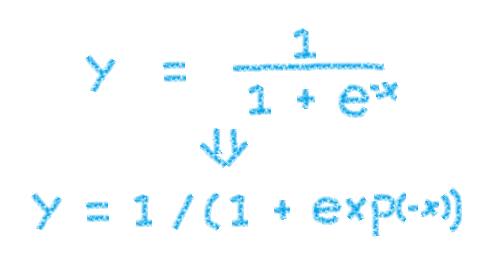
プログラマー的には↓こちらの方が見易いです。
y = 1 / (1 + exp(-x))エクセルで確認すると↓こんな感じになります。
x を入力すると y は0~1の間の値をとります。
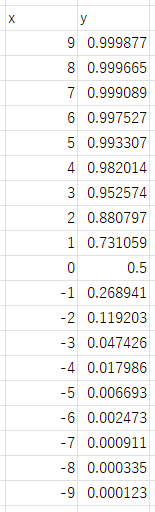
シグモイド関数を微分して 傾き をみてみようと思います。
言われているのは x 0近辺 が伸びが良い ということです。本当にそうなるのか検証してみます。
シグモイド関数は 合成関数 になっていて、いきなり微分することはできないので、これをパーツに分けます。
※合成関数の微分は、パーツに分けて→微分して→掛ける。
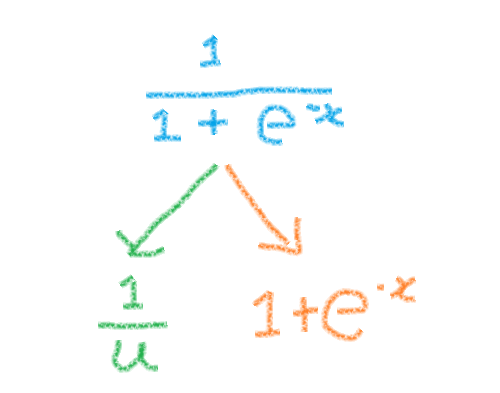
分母をuと置き換えました。
これなら微分することができそうです。1つづつ微分しています。
①分数の微分です。
マイナスを付けて、分母を2乗します。

②ネイピア数の微分です。
定数「1」は微分すると「0」になり、ネイピア数はマイナスを付けて指数の部分はマイナスのままです。
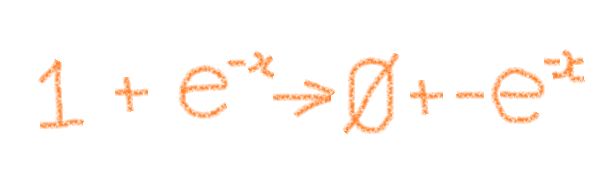
出てきたこれらの式を掛け合わせます。
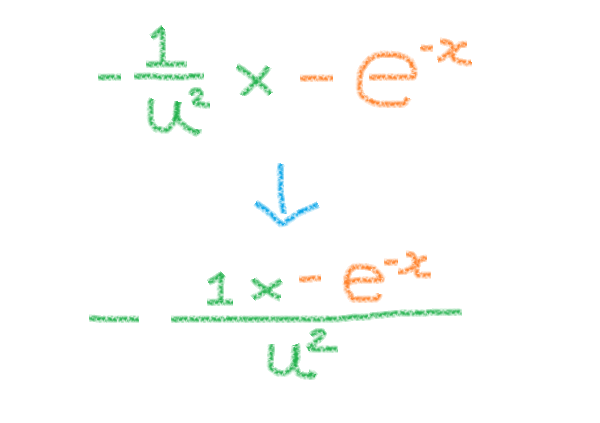
u に元の値(1+e^-1)を入れて、マイナスxマイナス→プラスをしたら式は完成します。
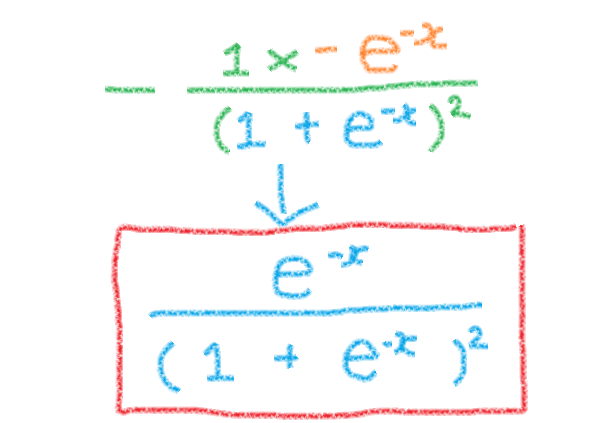
そういえば、微分の法則でこういうものがあります。

これを使えば良かったのかも。。。と後になって思いました。
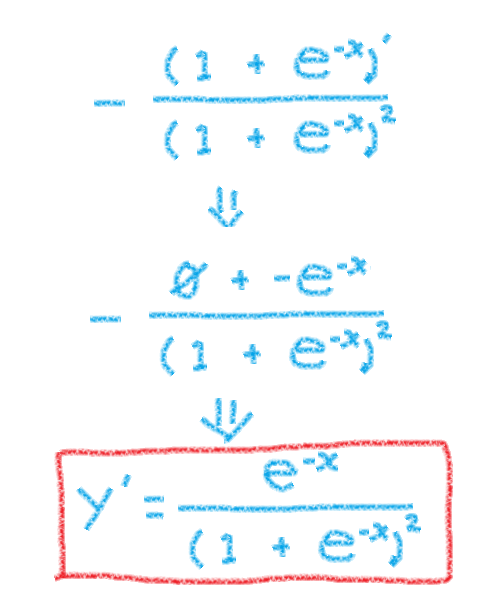
話を元に戻すと、シグモイド関数を微分したら↓この式ができた ということです。
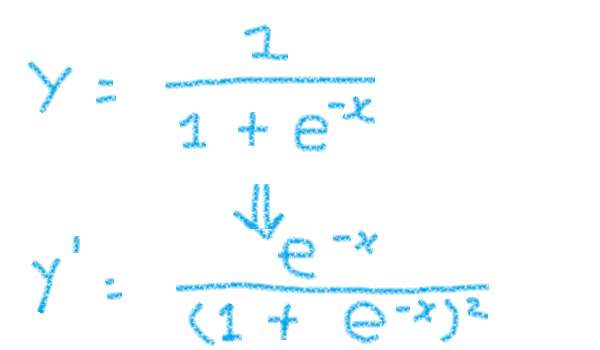
プログラマー的には↓こちらの方が見易いです。
y' = exp(x) / power( 1 + exp(x), 2 )エクセルにコピペしたところ、x が 0 の場合、傾きが 0.25 で一番伸びが大きい感じですね。
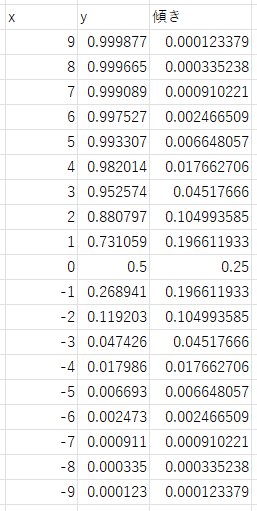
なんですけど…シグモイド関数の微分にはもっと良い方法(式)がありました「y * ( 1 – y )」(先人の知恵)。
※この y というのは、シグモイド関数を実行した結果です。
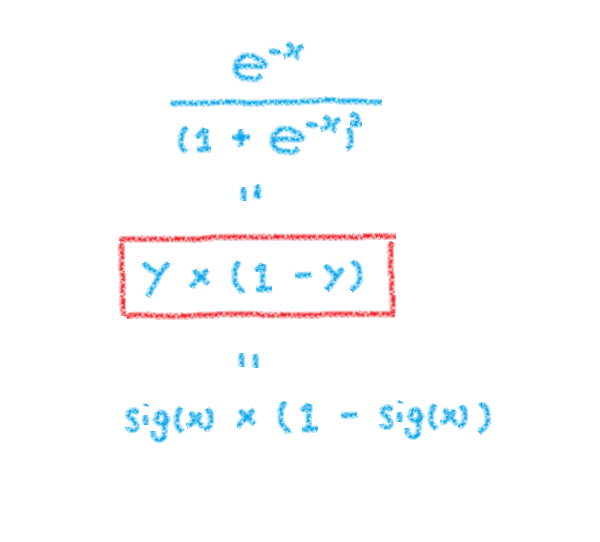
プログラマー的には↓こちらの方が見易いです。
y' = y * ( 1 - y )エクセルで検証としても同じ値になりました。
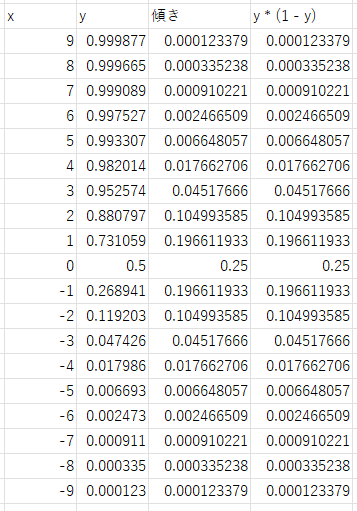
どうしたら、あの微分の式が「y * ( 1 – y )」になるのか?
ということで、ひとまず微分した式の分母を展開してみました。
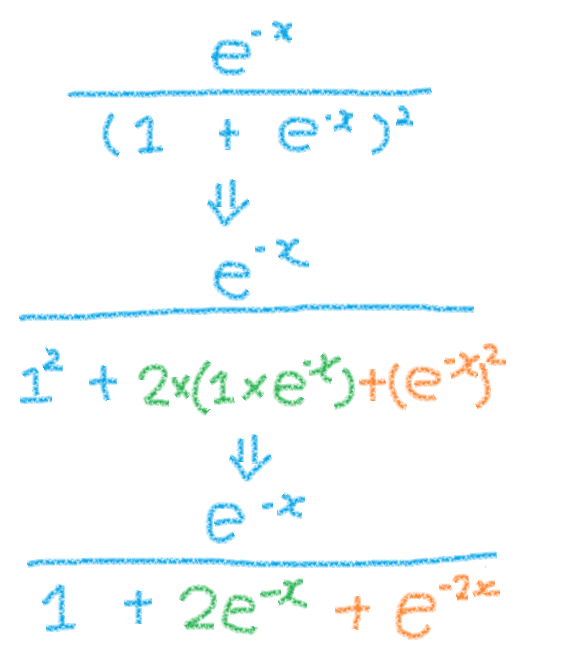
↑この式が目指す「ゴール」の式。
次に、ひとまず 先人の知恵 の↓下の式に シグモイド関数 の式を入れてみました。

↓y の部分にシグモイド関数を入れました。
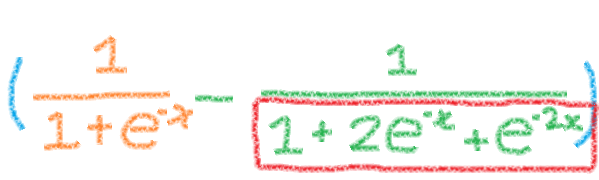
ここで「ピン」と来た!
さっきの「ゴール」の式 と比べると、右の緑の式の分母が同じ!これは(1+e^-x)の2乗。
ということで、左のオレンジの式の分子と分母に(1+e^-x)を掛けてあげればいけるかも。

これで分母がそろって引き算ができます。
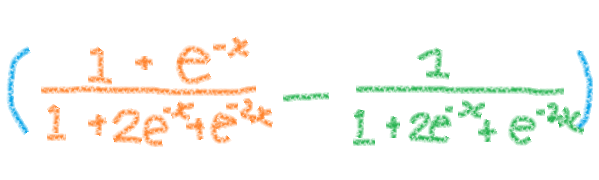
引くと 「ゴール」の式 と同じになりました。
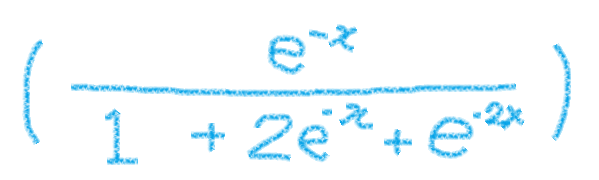
分母を因数分解して完成です。こういうことなのか
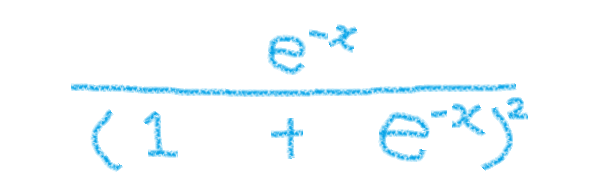
以上
と思ったけど、もっと簡単なやり方がありそうなのです・・・。

↑上の 先人の知恵 の式に シグモイド関数 の式を展開しないで入れてみました。
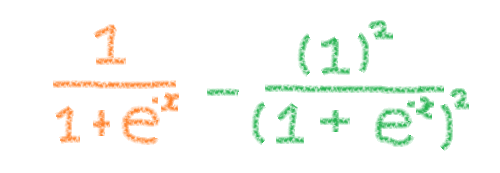
左のオレンジの式の分母を、緑の式に合わせるように(1+e^-x)を分子と分母に掛けて、引くと・・・できました・・・。
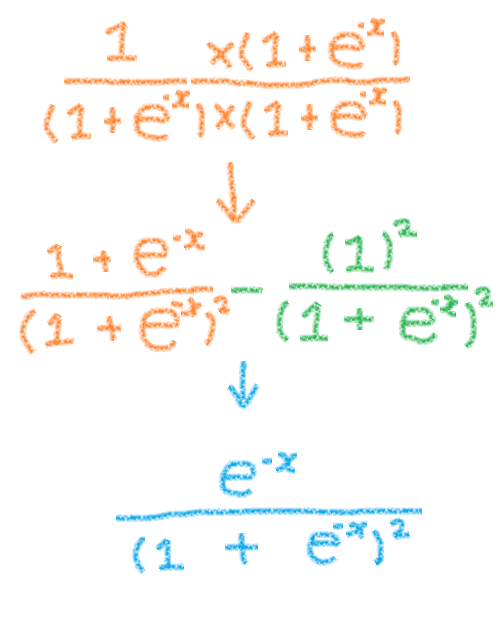
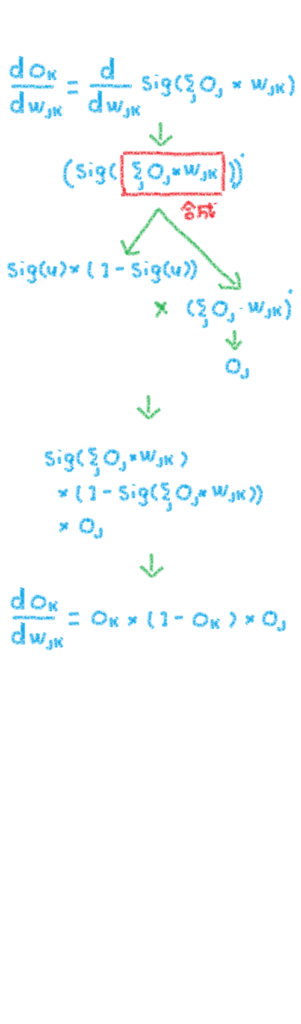
シグモイド関数の微分を使った例
以上